Etiqueta: Google

GoLang Newton Raphson.

GoLang es un «nuevo» lenguaje de programación en el cual estoy interesado ya que el programa de repositorios llamado Aptly está escrito en ese «idioma de computación» (gracias a Andrey Smirnov @smira). Ustedes pueden obtener información más precisa sobre este lenguaje de programación en este enlace que obtuve via Twitter:

Por ello lo estoy aprendiendo por medio de un tutorial y allí me encuentro con un método para calcular raíces cuadradas por aproximación según Isaac Newton el cual yo no conocía.

Introducción.

Como yo estudié ingeniería y las matemáticas me traen gratos recuerdos me puse a analizar la fórmula que proponen los desenfadados programadores y desenfadadas programadoras de Google (la tuve que nombrar ya que ésta empresa es la que lo patrocina) y definitivamente que no me gustó la fórmula que presentan y el método de programación para calcularla.

Mucha gente ha escrito sobre el tema, incuyendo Wikipedia, por supuesto, pero me pareció un método muy enrevesado, para mi gusto (la historia allí descrita me hace saber que en realidad lo inventó primero el matemático Joseph Raphson pero Newton llegó a la misma conclusión si saber nada del trabajo del otro matemático).

Me encanta ser práctico, ver ejemplos y lo que muestran en este enlace me pareció pulcro y limpio y a pesar que llevo AÑOS sin calcular derivadas y series se llega rápidamente a una solución en el ejemplo 2 (pero yo realmente me deleité con el ejemplo 1) .

Propuesta.

Basado en lo que me explican me propongo programar para calcular CUALQUIER raíz cuadrada de un número natural mayor a 1 y de una manera recursiva (a diferencia de como lo piden en el tutorial con 10 iteraciones) más sin embargo no he podido resolver el detalle de convertir dicha función en un objeto que sólo tengamos que pasarle el número a calcular su raíz cuadrada, la precisión en decimales, sin más desde afuera, como lo planteo siempre hay que modificarle adentro en la función.

Si más preámbulos (que no, que no vamos a estudiar en este post «Análisis Matemático I», II ni III, ni «Ecuaciones Diferenciales» ni «Matemáticas Aplicadas») le presento mi solución, con comentarios en castellano:

package main

import (
    "fmt"
    "math"
)

func NewtonRaphson(x float64, comienzo int, margen float64) float64 {
  var resp float64 = 0
  var z    float64
  var dif  float64
  //Cambiar z al entero cuadrado inferior a x para calcular
  //otras raices
  if comienzo == 1 { z = 1   }
  //fin semilla
  if comienzo == 0 { z = x }
  
  //Para calcular otra raíz cambiar el primer 2 por
  //el numero cuya raiz cuadrada se desea calcular    
  z = ( z + 2 / z) / 2
  dif = x - z
  
  
  if dif > margen {
    resp = NewtonRaphson( z , 0, margen)
  } else {
    resp = z
  }
  return resp
}

func main() {
    fmt.Println(NewtonRaphson(2, 1, 0.0000001))
    fmt.Println(math.Sqrt(2))
}

Obteniendo los siguientes resultados, los cuales se aproximan bastante, como ven:

1.414213562373095
1.4142135623730951

Program exited.

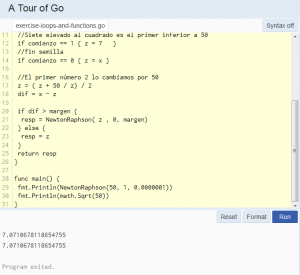
Si quisiéramos calcular la raíz cuadrada de 50 debemos hacer dos cambios en el programa (atención: si copian y pegan el código para probar, respeten el indentado):

package main

import (
"fmt"
"math"
)

func NewtonRaphson(x float64, comienzo int, margen float64) float64 {
 var resp float64 = 0
 var z    float64
 var dif  float64
 //Siete elevado al cuadrado es el primer inferior a 50
 if comienzo == 1 { z = 7   }
 //fin semilla
 if comienzo == 0 { z = x }

 //El primer número 2 lo cambiamos por 50
 z = ( z + 50 / z) / 2
 dif = x - z

 //Verifica el margen de error para finalizar el cálculo
 //y devolver el resultado
 if dif > margen {
  resp = NewtonRaphson( z , 0, margen)
 } else {
  resp = z
 }
 return resp
}

func main() {
 fmt.Println(NewtonRaphson(50, 1, 0.0000001))
 fmt.Println(math.Sqrt(50))
}

Y esto es lo que arroja el servidor remoto que ejecuta código:

AHORA BIEN ésta es mi primera impresión de este lenguaje (puede ser que esté equivocado), se parece bastante a Python, pero bueno, vamos a «seguirle dando a los hierros» y veremos en que consiste este lenguaje, prometo próximas entradas en este blog acerca del tema.

<Eso es todo, por ahora>.